Análisis matemático de una decisión sencilla. Ejemplo de por qué nos atrae intelectualmente el poker.
En este artículo voy a desmenuzar matemáticamente una de esas manos en las que nos vemos envuelto los jugadores de torneos de poker NL Texas Holdem habitualmente. Se trata de una mano en la que únicamente tenemos que tomar una decisión, pagar un all-in o no pagarlo (a priori de las más sencillas que nos podemos encontrar en este juego tan complejo).
Hemos jugado un torneo de 500 personas y nos encontramos en la fase final del mismo. Estamos entre los 6 últimos supervivientes.
Los stacks de los jugadores que quedan vivos (incluyéndonos como jugador 6) son los siguientes:
Jugador 1: 100.000 puntos.
Jugador 2: 110.000 puntos.
Jugador 3: 180.000 puntos.
Jugador 4: 90.000 puntos.
Jugador 5: 200.000 puntos.
Jugador 6*: 250.000 puntos.
Los premios para los primeros 6 clasificados del torneo son los siguientes:
Jugador 1: 4.000 €
Jugador 2: 2.500 €
Jugador 3: 2.000 €
Jugador 4: 1.500 €
Jugador 5: 1.000 €
Jugador 6*: 500 €
Con estos valores el valor en dinero de cada uno de estos stacks (empleando el método ICM: Independent Chip Model) sería el siguiente:
Jugador 1: 100.000 equivalen a 1.596,88 €
Jugador 2: 110.000 equivalen a 1675,04 €
Jugador 3: 180.000 equivalen a 2104,8 €
Jugador 4: 90.000 equivalen a 1512,81 €
Jugador 5: 200.000 equivalen a 2201,18 €
Jugador 6*: nuestros 250.000 puntos equivalen a 2409,3 €
La ciega pequeña tiene que poner 5.000 y la ciega grande 10.000, con un ante de 1.000 por jugador.
En la mano que vamos a analizar simulamos que nos reparten una pareja de dieces en la ciega grande. La mano le llega limpia al jugador 5 que es la ciega pequeña, mira sus cartas, y mete en el centro todas sus fichas. ALL-IN.
Con estos valores utilizando una calculadora de ICM, me sale que necesitamos una probabilidad de ganarle la mano o equity superior a 61,68% para que la mano tenga esperanza matemática positiva (EV+). Esto quiere decir que si tuviésemos justo un 61,68% de probabilidades de llevarnos la mano contra el rango REAL de push de nuestro rival, sería independiente el call o el fold. Si tenemos más de ese 61,68% de probabilidades es mejor el call y si tenemos menos de 61,68% contra el rango de manos en el que nuestro rival va all-in en esa mano sería mejor no jugar nuestra pareja de dieces.
Aquí está una de las diferencias entre el cash y los torneos. Si esta mano fuese de cash necesitaríamos una equity ligeramente inferior al 50% para que la mano fuese EV+. Esta diferencia es consecuencia del coste de confrontación o bubble factor que hay en los torneos y no en el cash.
Hasta este punto todo son matemáticas. Ahora viene lo subjetivo y lo más complicado del análisis: la estimación del rango de manos con el que el jugador 5 irá all-in. En este ejemplo, en base a mi experiencia y poniéndonos en el pellejo de un jugador regular de torneos de niveles medios, el rango de manos que estimo es el siguiente: (No entro a valorar cuál sería el rango óptimo de all-in del jugador 5, eso daría para otro artículo).
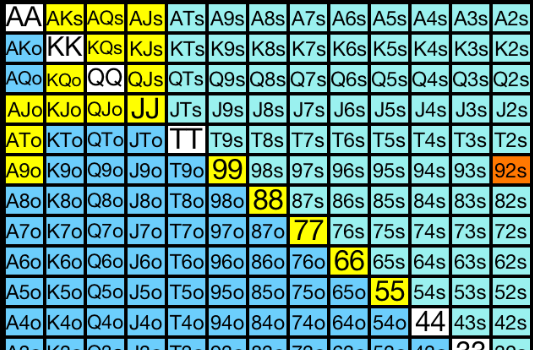
[AJ,AT,A9,KQ,KJ,QJ,99,88,77,66,55], independientemente de que sean o no del mismo palo. Suponemos que sus manos Premium: [AQ,AK,JJ,QQ,KK,AA], las sube a 2, 2,5 o 3 ciegas para inducir nuestro all-in con manos peores. Además no incluímos dieces para simplificar el cálculo porque es muy improbable que él los tenga también.
Pues bien, nuestra pareja de dieces contra su rango de all-in tiene un 62% de probabilidades de llevarse el bote. Por lo que la decisión correcta es pagar su all-in.
1. Si nos retiramos pre-flop nuestro stack valdría 2.367,36 €
2. Cuando pagamos y pedemos nuestro stack pasa a valer 1222,87 € (38% de probabilidad cuando pagamos).
3. Cuando pagamos y ganamos nuestros stack valdría 3.078,52 € (62% de probabilidad cuando pagamos).
Por lo tanto nuestro stack cuando pagamos = (1222,87 * 38% + 3.078,52 *62%) = 2.373,37 €, ligeramente mejor a nuestro stack cuando nos retiramos preflop.
Cada vez que foldeamos la mano en esta situación y no pagamos estamos perdiendo 6 euros siempre y cuando la estimación del rango con el que nuestro rival va all-in sea acertada.
Si en vez de una pareja de dieces tuviésemos una mano como nueves: y el rango con el que va all-in nuestro rival es [AJ,AT,A9,KQ,KJ,QJ,TT,88,77,66,55,] quitamos los nueves (por ser improbable que nuestro rival tenga esa mano) y ponemos los dieces con respecto al rango anterior – Obviamente el rango de all-in de nuestro rival es independiente a la mano que tengamos nosotros-. Tendríamos un 57,2% contra su rango por lo que la decisión correcta si tenemos 2 nueves en esa mano es tirarla al mazo. (me atrevería a apostar que la gran mayoría de vosotros pagaríais ahí con 99, yo mismo lo hubiese hecho antes de hacer todo este análisis). Estaríamos perdiendo unos 80 euros cada vez que pagamos con pareja de nueves el all-in del jugador 5.
Si cometemos el error de pagar en esta situación el all-in del jugador 5 con AT de distinto palo (50,4% de probabilidad de ganar frente a su rango) está decisión nos estaría costando de media a largo plazo 216 euros, casi el 10% del valor en dinero de nuestro stack en fichas. En cash, sin embargo, donde la relación entre las fichas y su valor en dinero es líneal sería correcto pagar con AT de distinto palo.
Aquellos gamblers que pagáis aquí incluso con pareja de cuatros (42% de probabilidad de ganar la mano frente al rango de all-in del jugador 6) os estaría costando de media a largo plazo 365 euros, que es el 15% del valor en dinero de vuestro stack.
Para terminar con el análisis, voy a hacer una mínima variación en los stacks iniciales dejando constante todas las demás variables. Imaginaros que el jugador 5 nos cubre en fichas. Pongamos que estos son los stacks iniciales:
Jugador 1: 100.000
Jugador 2: 110.000
Jugador 3: 180.000
Jugador 4: 90.000
Jugador 5: 200.000
Jugador 6*: 190.000
Los mismos stacks de partida de nuestros rivales, el único cambio es que nosotros en vez de tener 250.000 fichas, tenemos 190.000 y por lo tanto el jugador 5 nos cubre y nos deja fuera del torneo si pagamos y perdemos el bote.
En este caso necesitaríamos una probabilidad de ganarle de un 67% para que el call fuese rentable. Por lo que deberíamos retirarnos con manos como dieces (62% de ganar al rango de all-in de nuestro rival) e incluso AK del mismo palo (63,6% de probabilidad de derrotar al rango de all-in del jugador 5).
Eso sí, en este último caso, como el paradigma es diferente al cubrirnos en fichas el jugador número 5, éste si es un rival competente probablemente irá all-in con un rango de manos mayor que cuando no nos cubre, por lo que nuestra pareja de dieces o nuestro AK del mismo palo tendrá una probabilidad ligeramente mayor de derrotar a su rango cuando pagamos su all-in.









Hola Jorge:
Ante todo felicitarte x los articulos que dejas y x la web en general.
Esta semana he tenido una mano muy parecida a esta en el Sunday Special, vs el tipico jugador que reraiseaba todo x tener muchas fichas.
Mi situacion era 96/100 y cobraban 81, conb 9.6 ciegas creo recordar y asi se desencadeno la mano.
http://www.educapoker.com/foros/sng/estrategia-universidad/manos-torneos-multimesa-universidad/etapa-critica-10bb-tt-juego-burbuja#new
Me gustaria tu opinion sobre esta mano, ya que no paro de darle vueltas.
Un saludo.
Hola! Pues yo creo que es mejor foldear, pero no debe ser un error muy grave ir all-in.
Si quedáseis 82-90 jugadores si que vería el fold como mejor opción, pero con 100 vas mucho más apurado para poder entrar en premios. El problema es que la mano viene ya con un raise y un reraise… Si sólo viniese con un raise veo q es un push claro en la situación que planteas. Pero con el raiser y el 3betor me decanto por el fold.
Un saludo.